6. Utilisation des Normales
vendredi 4 janvier 2008, par Chris Young
Introduction
Comme vous avez pu le voir, un modèle est limité en termes de quantité de polygones. On ne peut donc pas reproduire parfaitement une courbure sur une surface. Il faudra donc passer par d’autres moyens pour éviter de nous retrouver avec un modèle trop visiblement anguleux.
La façon dont un modèle donne une impression de courbure est directement liée à la manière dont la lumière est "traitée" par ce modèle. Ce "traitement" a pris en Anglais le nom de shading, improprement traduit par "ombrage", on devrait dire "nuançage" (shade = nuance, shadow = ombre).
Rappel sur les lois de Snell & Descartes
Il me semble que ces lois sont au programme de seconde mais il n’est peut-être pas inutile de faire un rappel. ;-) Tout d’abord, situons le problème : nous avons une surface, sur laquelle vient se réfléchir un rayon lumineux. Il nous faudrait bien évidemment savoir comment sera dirigé le rayon réfléchi en fonction de la direction du rayon incident.
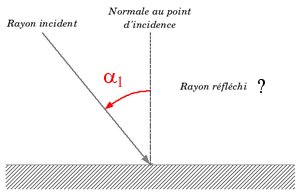
C’est ici qu’interviennent messieurs Snell et Descartes, qui nous disent ceci :
![]() « Le rayon réfléchi est contenu dans le plan d’incidence » (formé par le rayon incident
« Le rayon réfléchi est contenu dans le plan d’incidence » (formé par le rayon incident ![]() et la normale
et la normale ![]() à la surface)
à la surface)
![]() « L’angle formé entre la normale et le rayon réfléchi est égal à l’angle situé entre le rayon incident et la normale »
« L’angle formé entre la normale et le rayon réfléchi est égal à l’angle situé entre le rayon incident et la normale »
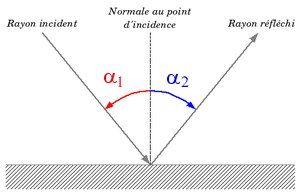
On a donc un rayon réfléchi de cette manière :
Comme notre surface sera rarement un miroir, il faut introduire un phénomène de diffusion. Il apparaît alors autour du rayon réfléchi principal d’autres rayons de plus faible intensité.
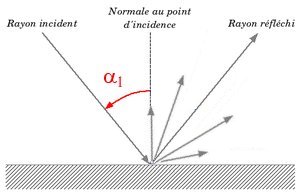
La quantité de lumière reçus par l’observateur est donc fonction de sa position par rapport à l’axe du rayon réfléchi principal. S’il est situé sur cet axe, la quantité de lumière sera maximale. Plus il s’en éloigne, moins il reçoit de lumière.
Flat shading et Gouraud shading
Quand le modèle comporte plusieurs faces, il y a alors plusieurs moyens de calculer la luminosité reçue. On considère l’objet fixe et la source de lumière fixe également, le rayon incident est donc constant. Le seul moyen de faire varier la direction du rayon réfléchi est donc de faire varier l’orientation de la normale. Dans la définition de Snell et Descartes, la normale est systématiquement orthogonale (perpendiculaire) à la surface sur laquelle se réfléchit le rayon. Avec cette définition, on a pour 3 faces le schéma suivant (en prenant la normale au centre de la face) :
![]() <
< ![]() <
< ![]() donc on affectera une luminosité plus forte à la face 1 qu’à la face 2, elle-même plus lumineuse que la face 3. On obsevera donc ceci :
donc on affectera une luminosité plus forte à la face 1 qu’à la face 2, elle-même plus lumineuse que la face 3. On obsevera donc ceci :

Comme vous pouvez le voir, les arêtes entre les faces sont très vives, et ce type de nuançage n’est clairement pas adapté pour représenter une courbure. Il fallut donc attendre le coup de génie d’un certain Henri Gouraud, chercheur en informatique français, qui publia en 1971 une méthode pour améliorer le rendu des courbures. Le Gouraud shading repose sur l’idée d’harmoniser les normales en chaques vertex commun à plusieurs faces, pour ensuite réaliser une interpolation de la luminosité calculée aux vertices pour le reste de la face. Je sais, ça peut paraître un peu obscur dit comme ça, on va donc reprendre avec quelques illustrations.
Premièrement, j’ai dit qu’on ne se plaçait plus au centre de la face mais aux sommets. On devrait donc avoir ceci :
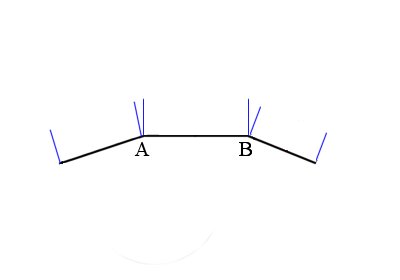
On voit qu’à chaque point A et B sont affectées deux normales, une par face ayant pour sommet le point en question. C’est de là que venait la discontinuité dans le flat shading. Ici pour assurer la continuité, on prend simplement à chaque vertex la moyenne des normales qui lui sont associées. Dans notre cas on obtient ceci (nouvelles normales en rouge) :
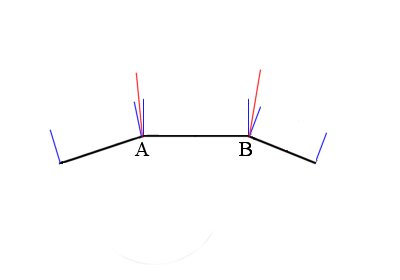
On calcule alors la luminosité en chaque point avec les lois de Snell et Descartes, et comme on a, pour une même face, différentes nuances de luminosité, on ne peut pas appliquer une teinte homogène sur chaque face. Au lieu de cela, on réalise une interpolation des nuances, qui donnera un dégradé de luminosité sur chaque face. Au final, on obtient ceci :

La version O² : sharp & smooth edges
Il s’agit maintenant de mettre en pratique dans O² ce que nous venons de voir. Dans O², les normales sont représentées par les petits "poils" bleus présents sur chaque vertex. Si vous ne pouvez pas les voir, vérifiez dans les Options d’O² que la ligne "View normals" est bien cochée.
La manipulation de ces normales est relativement simple. On modifie les normales sur une arête en sélectionnant les deux vertices qui la constituent et en appuyant au choix sur [U] pour avoir un flat shading ou sur [I] pour avoir un Gouraud shading. Dans O², ces types de rendus sont appelés respectivement sharp edge (arête aigüe) et smooth edge (arête lisse), ce qui est assez représentatif de leur emploi. Par défaut, dans O² les arêtes sont smooth : si on ne touche à rien on aura donc un modèle entièrement en Gouraud shading.
Lançons donc O² pour faire des expériences ! Créez par exemple un cylindre, en choisissant une taille de 1, un rayon de 1 et 10 "segments radius" : cela signifie que le tour du cylindre sera représenté par 10 faces. Supposons que l’on veut représenter un baril, il faut que le tour du cylindre soit le plus rond possible, mais que les faces en "bout" apparaissent bien planes. Allons voir dans Buldozer ce que ça donne :

Comme vous pouvez le voir, le rendu est assez mauvais (pour pas utiliser de termes scato ;-) ), Buldozer essaie de rendre un arrondi entre le tour du cylindre et le cercle de base, qui donne un résultat assez moche. C’est bien sûr dû au fait que O² fait par défaut des smooth edges.
Essayons maintenant en flat shading pour voir : allez dans O², sélectionner le modèle en entier, et appuyez sur [U]. La première chose que vous pouvez voir, c’est que dans O² les edges changent de couleurs. Elles deviennent plus sombres et plus épaisses quand on fait un flat shading. Ce sera bien pratique plus tard pour s’y retrouver dans un modèle entre arêtes franches et arêtes lisses.
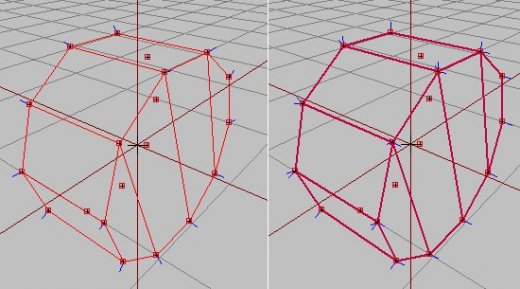
Allons maintenant voir dans Buldozer ce que ça donne :

On a maintenant des faces bien marquées aux éxtrémités du cylindre, mais les faces du tour sont bien trop marquées !
Il va donc falloir choisir quelles edges seront smooth ou sharp. Retournez dans O² et appuyez sur [I] pour tout repasser en smooth. Il faut alors uniquement sélectionner les edges qui constituent les cercles aux bases du cylindre. Soyez attentifs car c’est un peu subtil ! Si on sélectionne bêtement tous les vertices qui nous intéressent pour faire un sharp edge, vous vous rendrez bien vite compte que ça revient à tous les sélectioner et on retrouvera le rendu anguleux de tout à l’heure. Pour les premières fois, le mieux sera sans doute pour vous de sélectionner les vertices deux par deux pour faire le tour des deux cercles, mais en faisant attention on peut aller un peu plus vite. En effet il suffit de sélectionner les vertices qui nous intéressent en faisant bien attention qu’ils ne soient pas reliés entre eux par des faces, comme dans l’exemple suivant :
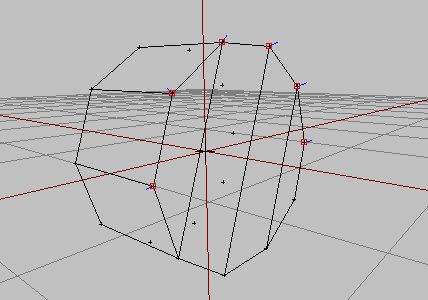
on les passe en sharp edge, puis on sélectionne les edges restants en faisant bien attention de bien sélectionner les points aux extrémités de le première fois, pour bien avoir toutes les edges :
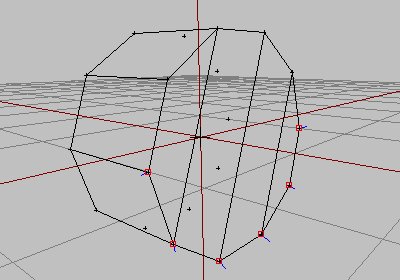
Si vous sélectionnez l’ensemble du cylindre dans O², vous devriez donc voir le tour de la base en couleur plus forte :
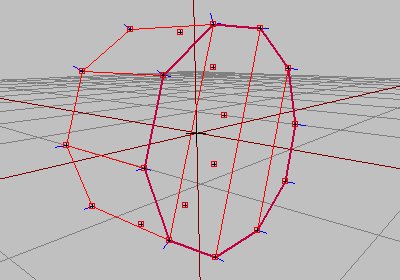
Faites de même pour la deuxième base, et nous avons maintenant un résultat bien meilleur sous O² :

Comme vous pouvez le voir, le tour du cylindre présente un dégradé correct pour représenter une courbure, et la liaison avec la base est plus franche. Pour que la base elle-même paraisse plus ronde (là j’avoue que c’est pas le top), il faudra augmenter le nombre de "segments radius" en créant le cylindre, mais cela consomme plus de polygones, c’est donc affaire de compromis entre l’ésthétique et le framerate.
Notes complémentaires
Juste quelques petites choses (relativement importantes quand même) que je ne savais pas où caser dans le tuto :
- Ne mettez en sharp edges que le strict minimum. Dans notre exemple il aurait été plus rapide de sélectionner toute une base du cylindre et de la passer en sharpen. Cela passait en sharp edges des lignes contenues dans une surface plane, dont le rendu aurait été exactement identique, mais comme le sharp edge sépare les normales des deux faces (même si elles sont confondues), chaque calcul de luminosité est fait deux fois pour rien. Donc rappellez-vous : les edges séparant deux faces coplanaires doivent rester en smooth.
- Après une rotation ou autre manipulation d’un objet dans O², les normales ne sont pas recalculées et le rendu sous Buldozer peut être très mauvais. Pour recalculer les normales et retrouver un bon rendu, appuyez sur [F5].